¿Cómo calcular el volumen de un cubo? Un viaje a la cuarta dimensión

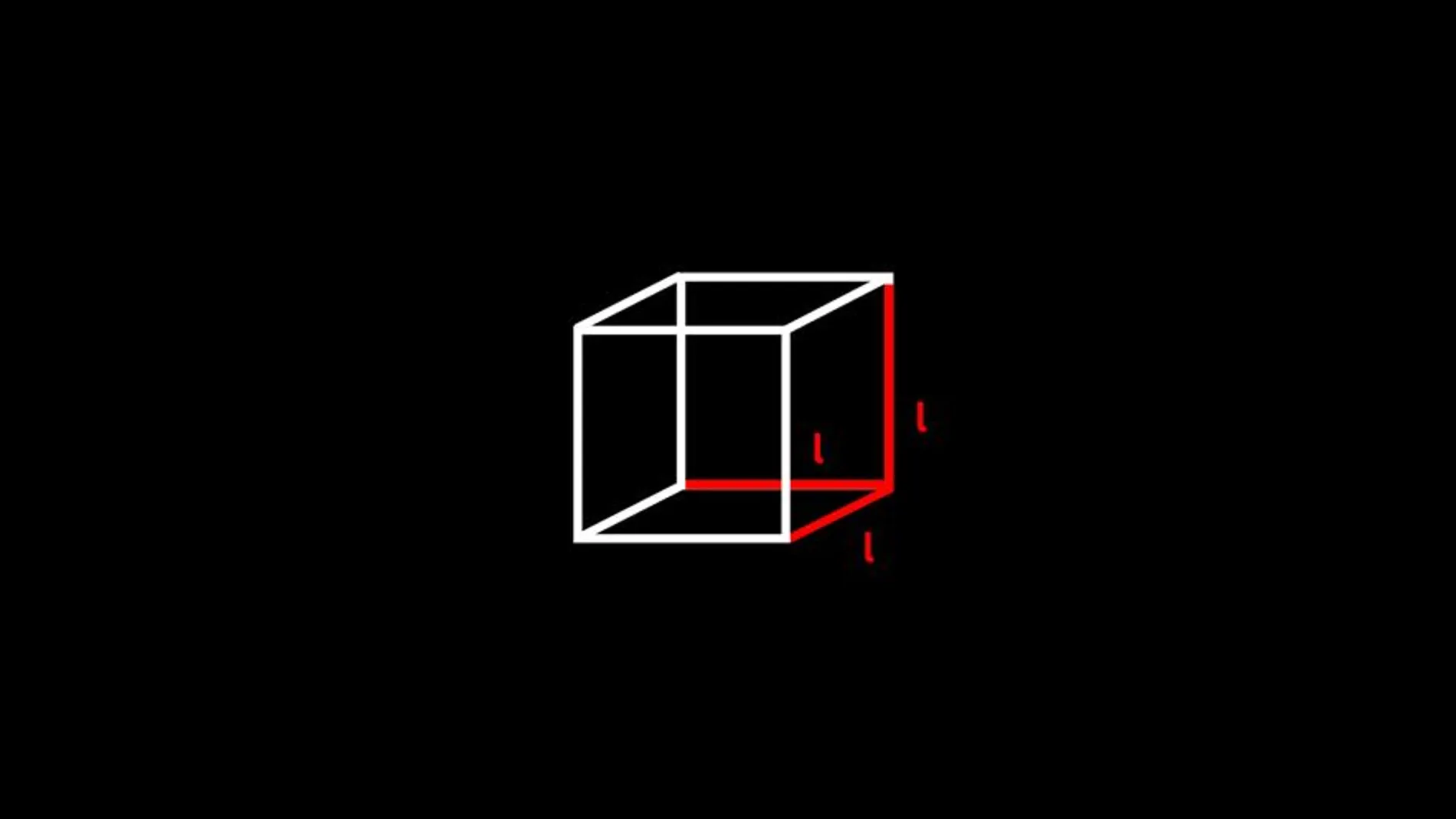
La pregunta con la que encabezamos este artículo es engañosamente fácil. Y digo “engañosamente” no porque su respuesta sea difícil, sino porque en un momento dado sí fue sumamente compleja. Ahora cualquier estudiante de secundaria sabe que, para calcular el volumen de un cubo, tan solo tenemos que tomar la medida de uno de sus lados y elevarla al cubo (lado por lado por lado). Aquí podría terminar el artículo, pero resulta que, si lo pensamos, nada de esto es tan evidente. ¿Por qué esta fórmula?No importa que sea intuitiva, hay que razonarla y, si nos detenemos a razonarlo, puede parecer hasta mágico que multiplicando tres números obtengamos un volumen. Sin saberlo, estamos utilizando una herramienta tremendamente sofisticada, una tecnología que no fue evidente y que supuso uno de los grandes avances de la humanidad.

Imagina que no supieras nada sobre geometría ni sobre unidades de medida. Te encuentras en un mundo cargado de objetos con su tamaño, sus distancias, sus pesos, pero solo puedes hablar de ello de forma muy aproximada. Dirás que algo es grande, extenso, pesado o que se encuentra lejos y, con suerte, podrás añadirle algún adverbio que particularice eso un poco, creando expresiones como “muy lejos”. Sin embargo, podemos estar de acuerdo con que tanto Beijin como Brasilia están “muy lejos” de Madrid y puede ser muy interesante que tengamos la capacidad de comparar esas distancias. Cierto es que podríamos decir: Beijin está más lejos de Madrid que Brasilia. Podríamos incluso añadirle un “bastante” para aludir a que la diferencia es notable. Hasta aquí nos hemos apañado bastante bien sin utilizar números.

Aunque tenemos un problema, porque ya hemos visto que este sistema crea frases imprecisas o engorrosas, una de dos, y que para hablar de un concepto tendríamos que relacionarlo siempre con otro. Es más,tenemos otro problema incluso más serio: con él no podemos calcular. Podemos saber que hemos de tallar un bloque de mármol más grande que determinado objeto y más pequeño que otro, pero ¿cuánto exactamente? ¿Cómo podría calcular la gasolina que me haría falta para llegar de aquí a Beijin? Todo es demasiado complicado, necesitábamos algo que hiciera más precisas nuestras mediciones. Claro que, aunque parezca mentira, dividir el mundo en unidades no era una decisión tan evidente, ni de lejos.

¿Dónde parto un mundo tan continuo?

¿Qué leñe es un metro en realidad? El mundo, a simple vista, parece continuo. Las superficies son lisas, aparentemente sólidas. ¿Cómo dividirlas entonces para tomar medidas de ellas? Nos encontramos ante un problema ligeramente filosófico y, aunque tal vez no se explicitara en aquellos tiempos primigenios, hay cierta barrera a la hora de dar con soluciones que no vemos en la propia naturaleza. Más adelante, habría pensadores griegos como Leucipo y Demócrito que propusieran un universo compuesto por partículas indivisibles, átomos, una suerte de unidad con la que estaría compuesto todo. Ahora sabemos que hay partículas subatómicas como quarks, electrones, fotones, y que las propias distancias tienen cierta unidad por debajo de la cual empiezan a suceder cosas extrañas: la distanciad de Planck. Estamos muy acostumbrados a intuir divisiones donde no podemos sentirlas. Y claro, las unidades de medida son previas al propio Leucipo y su primitivo atomismo.

La primera solución exitosa que encontramos no se embarró tanto, no consiguió dar con esa idea tan abstracta de unidad y se tuvo que conformar con unificar un poco aquellas comparaciones de las que hablábamos. Solo había que ponerse de acuerdo para usar la misma comparación. Algo que todos tuviéramos más o menos a mano y cuyo tamaño variara relativamente poco. La solución estaba en las partes del cuerpo humano. Un dedo, un pie, o la distancia desde el codo hasta el final de la mano abierta. Al fin podíamos dar unas medidas más o menos claras. Es más, pronto se dieron cuenta de que, como las cosas no medían 5, 6 o 200 pies exactamente, necesitaban algún tipo de subdivisión. Precisamente por eso empezaron a trabajar con conceptos como “medio pie”. Era más objetivo claro y preciso que el método anterior, pero todavía estaba lejos de lo que tenemos ahora. Para que la ciencia y la tecnología se revolucionaran haría falta mucho más.

¿Qué es un área?

Insisto, imaginemos que no supiéramos nada sobre nuestras actuales unidades de medida. ¿Cómo te enfrentarías a un área? Imagina que un padre quiere legar a sus hijos una superficie cultivable equivalente, pero sus tierras son irregulares, rectángulos de distintas proporciones ¿Cómo las compararías? El ojo puede engañarnos y queremos ser justos. Lo más elegante que encontraron nuestros antepasados remotos fue algo parecido al pletro griego, que se refería al área que era capaz de arar una pareja de bueyes en un día. Era una medida práctica, pero confusa.

Puedes intentar medir cada lado de esa área con las unidades de longitud que acabamos de ver, pero eso nos daría varias medidas independientes. ¿Cómo las relacionarías entre sí? Más perímetro no significa necesariamente más área… Necesitaríamos que la geometría se desarrollara un poco y que demostrar que tiene una fórmula capaz de convertir esas medidas en un único número que dé buena cuenta del área real. Que efectivamente, si le aplicas una fórmula a un triángulo y otra a un cuadrado el resultado de ambas fuera comparable y no nos hiciera caer en engaños. Esta geometría básica, en su momento, fue alta tecnología.

Imagina que das con una fórmula aparentemente correcta ¿Cómo podrías demostrarla para quedarte satisfecho? Ahora tenemos métodos matemáticos y computacionales de todo tipo, pero por aquel entonces se estilaban las demostraciones físicas. Pensemos que, en lugar de codos o pies, tomamos como unidad de medida un objeto cuadrado, tan ancho como largo. Ahora, si queremos medir el área de una parcela rectangular, solo tendremos que ver cuántos cuadrados caben en ella, unos pegados a otros. Al ser rectangular habrá filas y columnas de cuadrados y sabemos que hay un método para ahorrarnos contar cada uno de ellos, multiplicar las filas por las columnas, esto es, los cuadrados de un lado por los del otro. O, dicho de otro modo: multiplicar lado por lado.

Ya no hacía falta cubrirlo con cuadrados, sino medir, con cualquier unidad, el largo de dos lados contiguos. Y claro, esta fórmula extensible a cualquier paralelepípedo (figuras de cuatro lados paralelos dos a dos) puede particularizarse para los cuadrados, donde sabemos que todos sus lados son igual de largos y sintetizar aquello de “lado por lado” en, simplemente “lado al cuadrado”. Más o menos así podemos entender la aparición de estas formas de medir el área. Sin embargo, todavía no hemos hablado de los volúmenes, y ese es, precisamente, el siguiente paso.

Engañosamente fácil

Y al fin llegamos al volumen, posiblemente el más sencillo y el más complejo a la vez. Más complejo porque civilizaciones como la griega decidieron que, no solo necesitaban esas nada sistematizadas y caóticas subdivisiones donde una medida era, por ejemplo, 144 veces más que otra, sino que muchas unidades eran diferentes en función de si medían el volumen de un sólido (grano, por ejemplo) o de un líquido. Por la contra, es más sencillo porque la unidad venía dada. Entendían que necesitaban un objeto de referencia que pudieran llenar con grano, o líquido, por ejemplo, una cotila, una taza pequeña que podía encontrarse en casi cualquier casa. De hecho, la cotila era una de esas unidades comunes tanto a volúmenes sólidos como líquidos. Ahora, todo lo que tenían que hacer era ver cuántas cotilas hacían falta para contener el mismo volumen que querían medir y todo solucionado.

La idea es buena y, de hecho, es un precursor de nuestros litros. El caso es que el litro no es la unidad que solemos utilizar para medir el volumen de un cubo, nuestro Sistema Internacional de Unidades toma como referencia el metro cúbico. No debería sorprendernos, porque es el siguiente paso lógico de esta sucesión. Ya hemos explicado cómo podían medir la longitud con su análogo de los metros, cómo los multiplicaban para obtener algo parecido al metro cuadrado con lo que medir áreas y, ahora, solo había que volver a multiplicarlo para tenerlos al cubo. La situación es muy parecida, solo que ahora, en lugar de un parterre, queremos medir el volumen de un bloque de mármol. Podemos hacer cubos pequeños y colocarlos hasta crear una pila con la misma forma y tamaño que la que queremos medir. Contando los cubos tendremos una medida de volumen.

La simplificación está clara, para evitar contar todo, resulta que podemos hacer lo mismo que con la superficie. Si multiplicamos cuántos cubos hay de lago y de ancho en la base de nuestro montón, podremos calcular cuántos hay en la capa inferior (su superficie) y, si lo multiplicamos de nuevo por cuántas capas hay (cuántos cubos hay en altura) obtendremos el número total de cubos, el volumen. Así que la fórmula para obtener el volumen de un prisma de base cuadrangular (un ladrillo de las proporciones que sean) será tan sencillo como multiplicar la longitud de tres de sus lados contiguos.

Y, una vez más, como todos los lados de un cubo miden lo mismo, podemos particularizar la fórmula para decir que el volumen de un cubo es su lado elevado al cubo (valga la redundancia). Ya tenemos la fórmula, pero el viaje no ha terminado, porque ¿qué pasa si elevamos el lado a cuatro en lugar de a dos o a tres? ¿Qué tipo de figura tendría un volumen que se calculara multiplicando lado por lado por lado por lado? Bienvenidos a la cuarta dimensión.

Una cuarta dimensión

Los matemáticos, que son los reyes de la abstracción, pronto entendieron que no tenían por qué limitarse a lo que es real, sino que pueden desarrollar su ciencia hasta las últimas consecuencias y explorar a dónde les lleva la lógica. En este caso, la progresión “línea-cuadrado-cubo” hemos visto que puede relacionarse uno a uno con “1 dimensión-2 dimensiones-3 dimensiones” y que la forma de medirlos es “lado-lado al cuadrado-lado al cubo”respectivamente. Si seguimos la serie y hablamos de un objeto imaginario que, para medirlo, necesitáramos elevar su lado a cuatro, podemos deducir cosas sobre él siguiendo el resto de las series. A todas luces parece que estuviéramos hablando de un objeto de cuatro dimensiones espaciales, largo, ancho, alto y vete tú a saber qué.

Esa es parte de la magia de estas ciencias formales, no necesitamos imaginarlo ni que sea real, solo que sea coherente con las matemáticas. Sea como fuere, esa cuarta dimensión debería ser perpendicular a las otras tres, del mismo modo que para pasar de una línea a un cuadrado añadimos una dimensión perpendicular (en 90º respecto a la otra) y para pasar de un cuadrado a un cubo lo extendemos en una nueva dirección igualmente perpendicular a las dos anteriores. Nosotros, que somos seres que viven y aprenden en un universo de tres dimensiones espaciales (y una temporal), no podemos hacernos una idea de cómo será esa cuarta dirección perfectamente perpendicular a la altura, la profundidad o la anchura.

Esa despreocupación por la realidad es la que nutre al chiste (no necesariamente gracioso) en el que un físico le pregunta a un matemático cómo consigue imaginarse objetos de veinte dimensiones y el matemático le responde que en realidad es muy fácil, solo tiene que imaginar tres dimensiones y añadir otras 17. En cuanto a esa tercera secuencia que hablaba de líneas, cuadrados y cubos, son solo los nombres que usamos para referirnos a ellos y cualquier cosa consensuada es igual de válida. En este caso, solemos usar el prefijo “hiper” para referirnos a esos objetos de cuatro dimensiones. Hipercubo, en este caso, pero también existiría una hiperesfera, por ejemplo. Otro nombre para el hipercubo que es mucho más popular entre el público es el de “teseracto”, que se ha abierto camino hasta el cine, apareciendo en Interestellar o a lo largo de la saga de Los Vengadores.

Eso sí, que no podamos imaginarlo a la perfección no significa que no existan trucos para ayudarnos a visualizarlo. Uno es utilizar esa dimensión temporal de la que no hemos hablado para proyectar en ella la cuarta espacial que no nos encaja en ningún lado. El resultado es un objeto en movimiento, que cambia constantemente siguiendo unos criterios matemáticos precisos y representando así esas cuatro dimensiones. Nada hemos hablado del otro paso clave de este proceso, la unificación de las muchas unidades de medida en un mismo sistema decimal, capaz de subdividirlas mediante una progresión más lógica y manejable (metros, decímetros, centímetros, milímetros…) Pero, a pesar de esa omisión, hemos podido ver cómo, detrás de una de las fórmulas más conocidas de la geometría elemental, se encuentra un proceso de abstracción nada trivial, algo que llevó tiempo perfeccionar y que nos abrió un mundo de aplicaciones. Porque tras la fórmula del cubo, lo que hay, es la firma de una de las mayores revoluciones de la humanidad.

QUE NO TE LA CUELEN:

• El proceso histórico ha sido simplificado y no fue igual en todos los lugares donde se desarrollaron estas medidas, pero ayuda a hacerse una idea de la cantidad de pasos y razonamientos inéditos que hubieron de seguir nuestros antepasados para llegar a algo que, para nosotros, es absolutamente elemental. Así pues, aunque los detalles son correctos, en estos planteamientos cronológicos de las ideas suele haber un grado de especulación nada desdeñable que debemos tener en cuenta.

REFERENCIAS (MLA):

• Gee, H., 2008. That extra dimension. Nature Physics, 4(5), pp.341-341.
• Klein, H., 2012. Science of Measurement. Dover Publications.
• Stewart, I., 2012. Historia de las matemáticas. Barcelona: Crítica.